How To Find Slope Of Hyperbola

Conics: Hyperbolas: Finding Data
From the Equation (page 2 of 3)

Sections: Introduction, Finding data from the equation, Finding the equation from information

Detect the heart, vertices, foci, eccentricity, and asymptotes of the hyperbola with the given equation, and sketch:

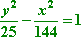
Since the y part of the equation is added, then the middle, foci, and vertices will be above and below the center (on a line paralleling the y -centrality), rather than side by side.

Looking at the denominators, I see that a ² = 25 and b ² = 144 , so a = 5 and b = 12 . The equation c ² � a ² = b ² tells me that c ² = 144 + 25 = 169 , so c = 13 , and the eccentricity is eastward = xiii/five . Since x ^two = (x � 0)^two and y ² = (y � 0)² , and so the centre is at (h, yard) = (0, 0) . The vertices and foci are above and below the center, so the foci are at (0, �xiii) and (0, 13) , and the vertices are at (0, v) and (0, �5) .

Considering the y part of the equation is dominant (existence added, not subtracted), then the gradient of the asymptotes has the a on top, so the slopes volition exist m = � 5/12 . To graph, I first with the center, and draw the asymptotes through it, using dashed lines:
Then I draw in the vertices, and rough in the graph, rotating the paper as necessary and "eye-balling" for smoothness:
Then I draw in the concluding graph every bit a smashing, smooth, heavier line:

And the balance of my answer is:

center (0, 0) , vertices (0, �5) and (0, 5) , foci (0, �13) and (0, thirteen) ,
eccentricity , and asymptotes

Requite the centre, vertices, foci, and asymptotes for the hyperbola
with equation:

Since the ten part is added, then a ^two = sixteen and b ^two = ix , so a = 4 and b = 3 . Also, this hyperbola's foci and vertices are to the left and right of the center, on a horizontal line paralleling the 10 -axis.

From the equation, clearly the centre is at (h, k) = (�3, 2) . Since the vertices are a = four units to either side, and so they are at (�7, ii) and at (1, 2) . The equation c ² � a ² = b ² gives me c ² = nine + 16 = 25 , so c = 5 , and the foci, being 5 units to either side of the middle, must be at (�eight, 2) and (2, 2) . Copyright � Elizabeth Stapel 2010-2011 All Rights Reserved

Since the a ⁱⁱ went with the 10 part of the equation, and then a is in the denominator of the slopes of the asymptotes, giving me g = � 3/iv . Keeping in mind that the asymptotes go through the center of the hyperbola, the asymptes are and then given by the straight-line equations y � 2 = � (three/4)(x + iii) .

center (�3, 2) , vertices (�7, 2) and (1, ii) , foci (�8, two) and (ii, 2) ,
and asymptotes

Find the heart, vertices, and asymptotes of the hyperbola with equation
four x ² � v y ^two + xl x � xxx y � 45 = 0 .

To find the information I need, I'll first take to convert this equation to "conics" form by completing the square.

fourx ⁱⁱ + 40x � 5y ² � xxxy = 45
4(x ^two + tenten ) � 5(y ² + 6y ) = 45 + 4( ) � 5( )
4(x ² + 10x + 25) � 5(y ² + viy + 9) = 45 + four(25) � v(nine)
4(10 + v)² � 5(y + three)² = 45 + 100 � 45

So the center is at (h, k) = (�5, �three) . Since the x role of the equation is added, so the center, foci, and vertices lie on a horizontal line paralleling the ten -axis; a ^two = 25 and b ² = 20 , and then a = v and b = 2sqrt[5] . The equation a ⁱⁱ + b ⁱⁱ = c ² gives me c ² = 25 + 20 = 45 , and then c = sqrt[45] = 3sqrt[5] . The slopes of the 2 asymptotes will exist grand = � (2/5)sqrt[v] . So my complete reply is:

centre (�v, �3) , vertices (�ten, �three) and (0, �3) ,

foci and ,

and asymptotes

If I had needed to graph this hyperbola, I'd have used a decimal approximation of � 0.89442719... for the slope, merely would accept rounded the value to something reasonable like m = � 0.9 .

<< Previous Top | ane | 2 | 3| Return to Index Next >>

Cite this article equally:

Stapel, Elizabeth. "Conics: Hyperbolas: Finding Information From the Equation." Purplemath.
Available from https://www.purplemath.com/modules/hyperbola2.htm.
Accessed